February 9, 2022

Add “validity” flag to TournamentGroup

To support my camouflage work, I needed to better handle the case where a Tournament fails to establish a partial ranking of its member Individuals. In the camouflage simulation, the “predator” needs to pick one of three camouflaged “prey.” The predator makes its selection by specifying a location in the image: the human user via a mouse click, the deep neural net computes an xy value.

But what happens if that location is not inside any of the three prey? If it is a clean miss? This rarely happens with a human predator. But it is common with a poorly-performing neural net predator. In this case, I want the predator to be the “loser” — and all three prey to survive — on the theory that they all fooled the predator. Before this change, one of the three prey would be declared the loser, effectively at random (based on selection order).

I modified TournamentGroup to add a bool flag for “validity” along with corresponding accessors getValid() and setValid(). All TournamentGroup objects are valid until explicitly set to be invalid.

This allows (say) a TournamentFunction to decide that the current tournament is invalid and should be canceled. Population::evolutionStep() will now leave the population unchanged if given a TournamentGroup which has been marked invalid.

March 25, 2021

Weighting selection of functions for initial random trees

When creating the initial Population of Individuals, the FunctionSet is filtered to a collection of GpFunctions with the required return type, and which can terminate GpTree construction (get to terminals) given the remaining tree “size.” Previously: one element of the filtered collection was chosen by uniform random selection. Now that happens by default, but the c++ initializer for  GpFunction can include an optional extra fifth argument, a float, indicating a selection weight other than one. Here for example is the “toy” example used in a new unit test. Each of the four listed GpFunctions is half as likely to be selected as the next one:

// Define FunctionSet with random selection weightings.
FunctionSet fs = { { { "Int", 0, 9 } },
                   { { "L", "Int", {"Int"}, ..., 0.5 },
                     { "M", "Int", {"Int"}, ..., 1 },
                     { "N", "Int", {"Int"}, ..., 2 },
                     { "O", "Int", {"Int"}, ..., 4 }, }, };

Adds new FunctionSet::weightedRandomSelect(), GpFunction::selectionWeight(), and UnitTests::gp_function_weighted_select().

January 29, 2021

Back and forth on random tournament member uniqueness

Back on October 14 I wrote a Population::selectThreeIndices() to pick indices of three random Individuals to form a random tournament. Its purpose was to guarantee the three Individuals were unique. This was to prevent forming a competitive tournament between, say, individuals 57, 83, and 57. I am paranoid about “try until success” algorithms getting stuck in infinite loop. But then I was also hinky about the statistical properties of my non-iterative solution. Eventually I decided that when selecting three items out of a collection of about 100, the frequency of duplication seemed low enough to ignore, so I just got rid of selectThreeIndices(). (To be sure, there are non-iterative, statistically neutral solutions to this, they just seemed a bit too heavy-weight to me. My intuition is famously unreliable.)

Later “subpopulations” (SubPops, breeding demes) were introduced. Now three Individuals were being selected from of group of 20-25. When I started running interactive Camouflage tests, it was visually obvious that a fair number of tournaments contained duplicated Individuals. So today I brought back a different implementation of selecting three unique indices called Population::threeUniqueRandomIndices(). This uses the evil “try until success” approach, but is liberally sprinkled with calls to assert() meant to catch any misbehavior, including getting stuck in the loop.

January 17, 2021

Upper and lower bounds on tree size during crossover

As suggested on January 12 LazyPredator now supports both anti-bloat and “pro-bloat” — that is, both upper and lower bounds on the size of trees created during crossover. In the “tree size agnostic case” GP crossover leads to slow but steady growth in population-average tree size. (That is: the GpTree::size() of each Individual, averaged over the Population, grows over time.) Recently I added a size-reducing bias to crossover when the parent trees are too large. Now the corresponding size-increasing bias is implemented when parent trees are too small. These limits can be set to infinity and zero to deactivate the size biases, but currently default to 150% and 50% of the given parameter for initial random tree max size. So for an initial max random tree size of 100, the size of trees during the run would be on the range [50, 150].  The limit values can be read or written which these member functions on a Population instance:

Population::getMinCrossoverTreeSize()
Population::setMinCrossoverTreeSize()
Population::getMaxCrossoverTreeSize()
Population::setMaxCrossoverTreeSize()

// Update February 3, 2021:
// New Population constructor allows these values to be specified initially:
Population(int individual_count,
           int subpopulation_count,
           int max_init_tree_size,
           int min_crossover_tree_size,
           int max_crossover_tree_size,
           const FunctionSet& fs)

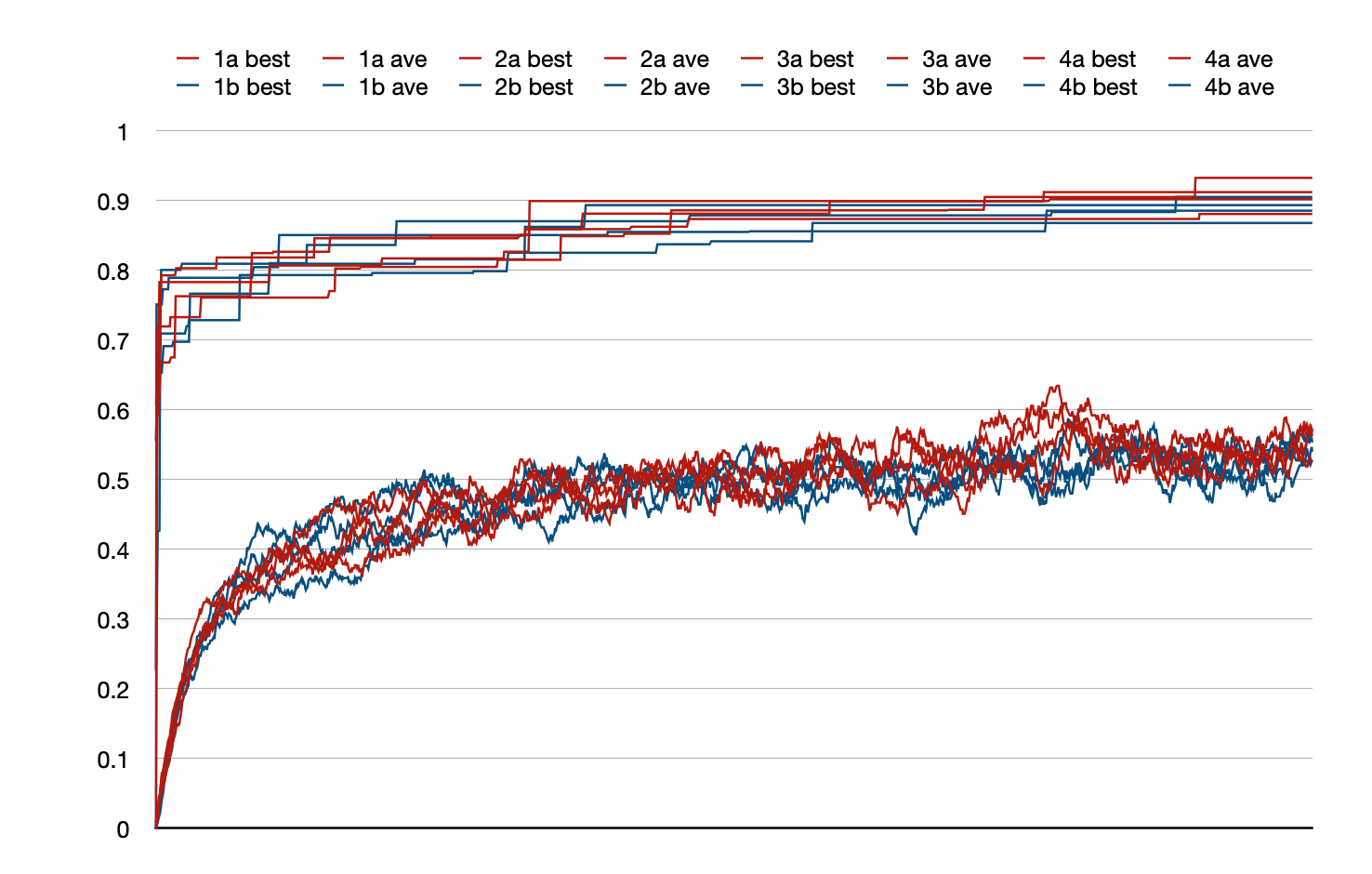
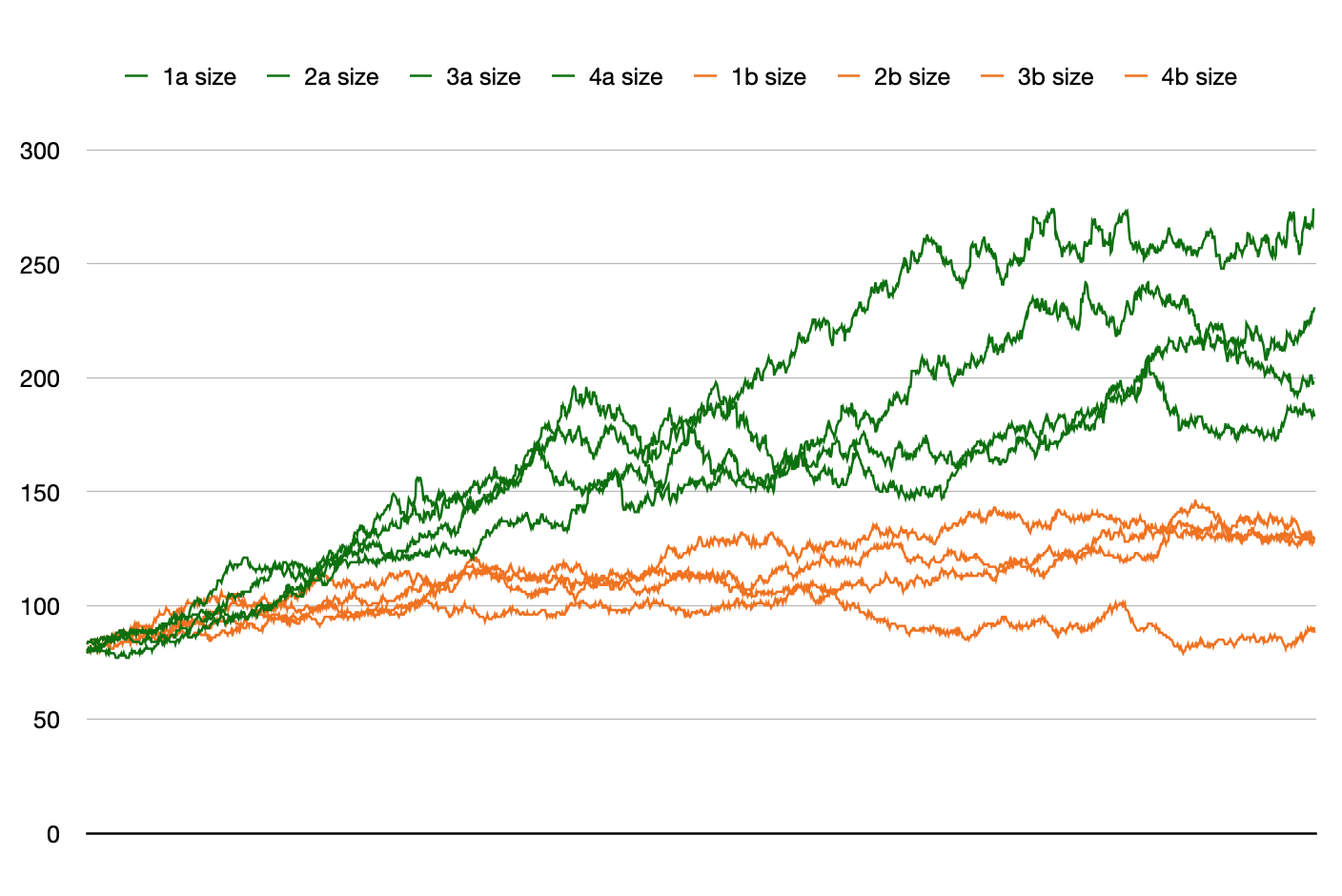
Here are eight LimitHue runs, four (red) with no limits, and four (blue) with limits set to enforce tight bounds on tree size. The only thing to see here is that reds and blues are roughly the same:

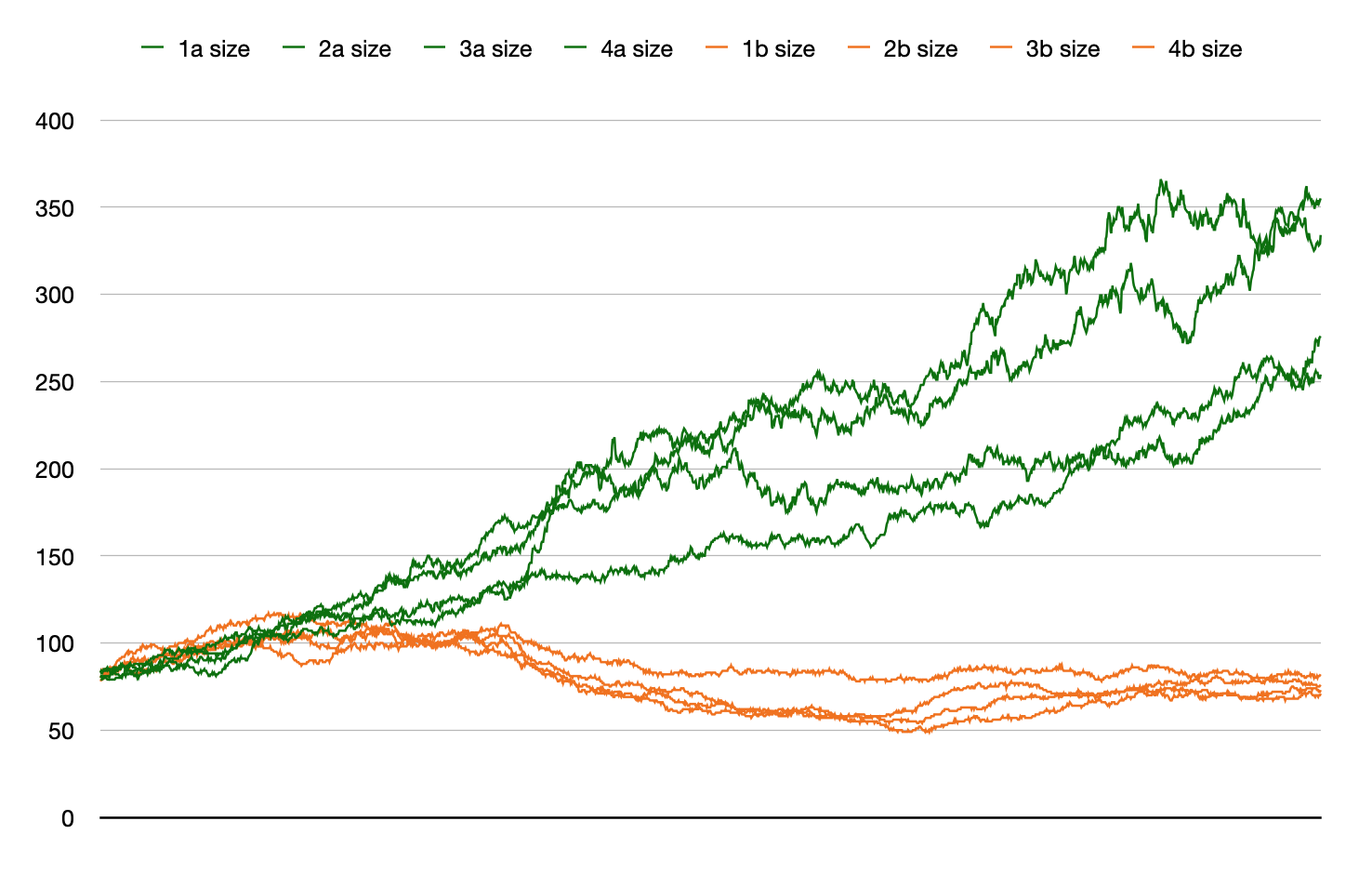
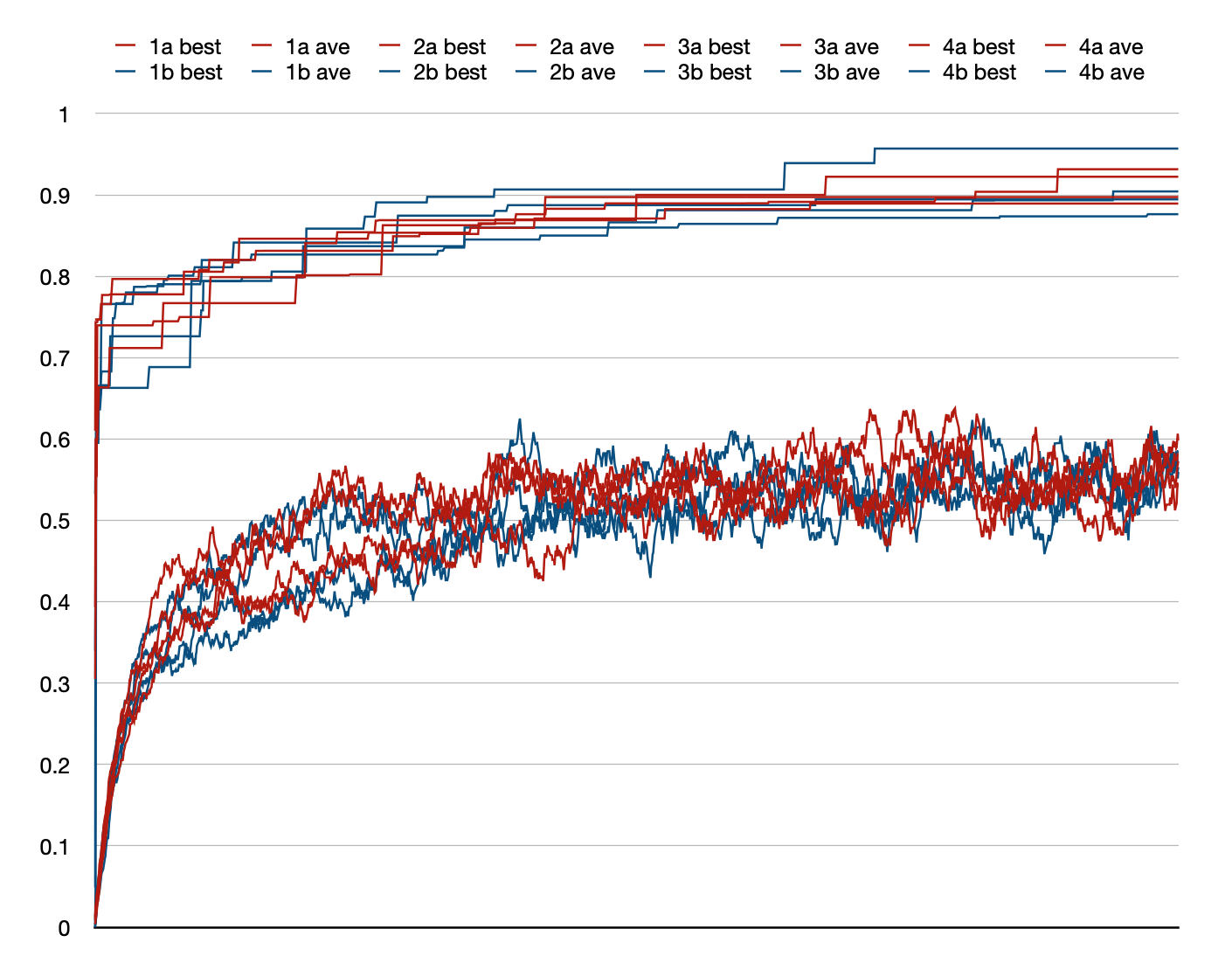
While the fitnesses are about the same in these two conditions, the no-limits condition (green) show steady growth in tree size, with limits (orange) stay within a narrow range:

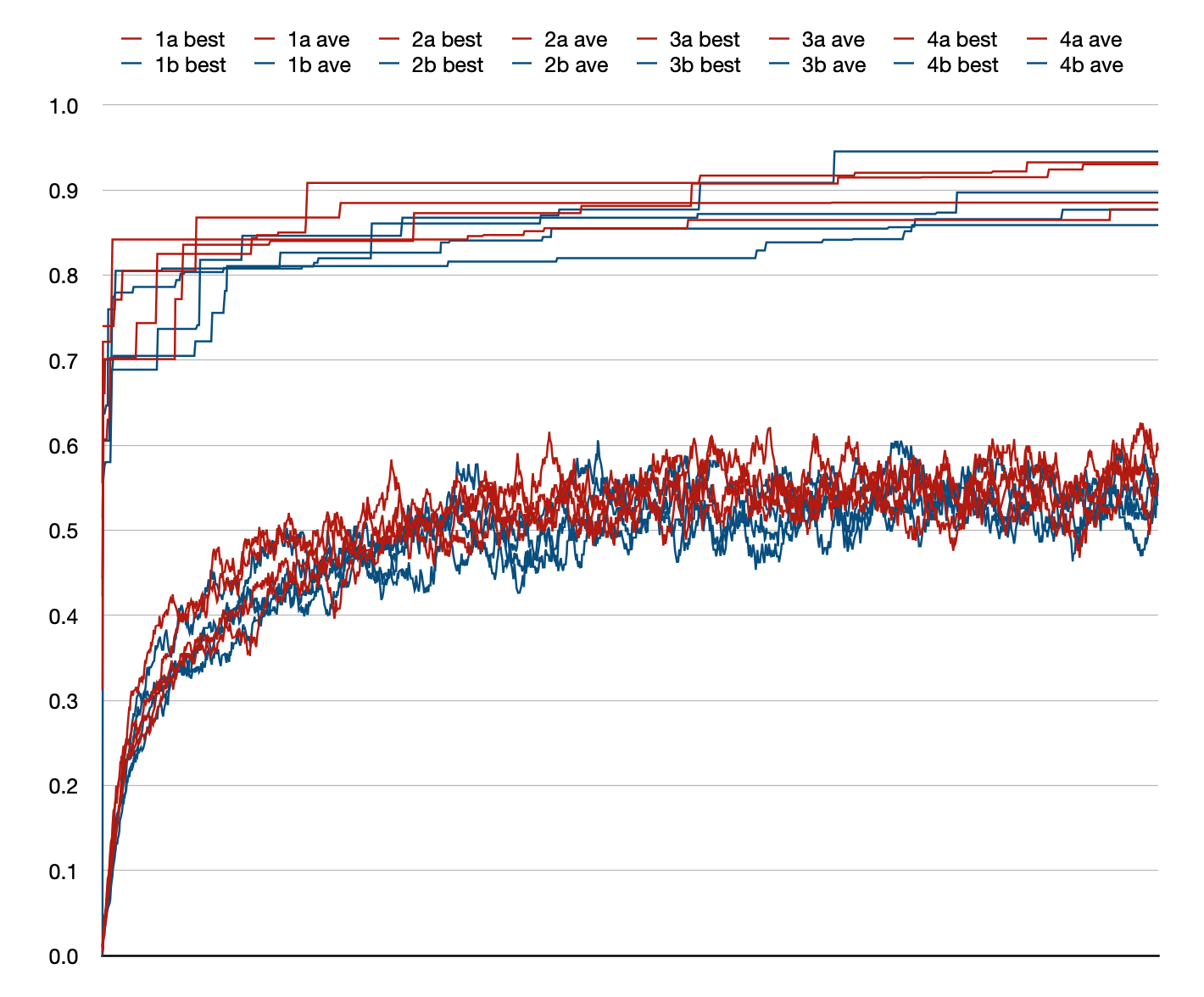
Here we zoom in on the bounded case (orange) to better see the vertical scale. Not only are the allowed tree size values in a narrow range, I also shifted this range twice during the run. For the first ⅓ of the run, the size bounds are [100, 110]. So if the parent tree is smaller than 100 (nodes) or bigger than 110, then size bias kicks in. For the second ⅓ of the run, the size bounds are [40, 50]. For the final ⅓ of the run, the size bounds are [70, 80].

The result is less crisp than I imagined. When (say) the upper bound is crossed, the “offspring” is made to be smaller, but can be much smaller. Perhaps with the upper and lower bounds set so close (10 nodes) the bias was being used almost each crossover, in opposite directions.

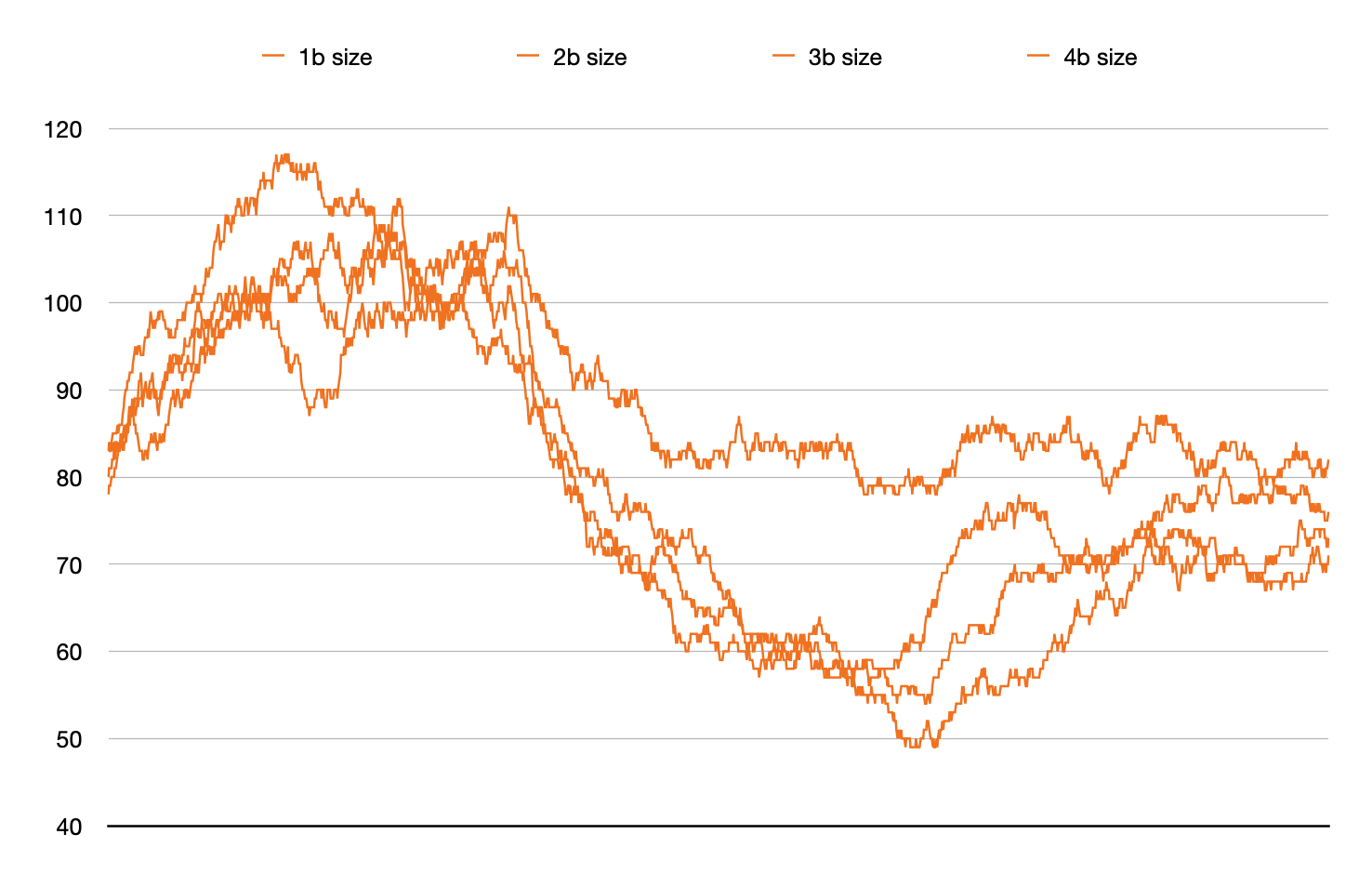
January 12, 2021

Size limitation during crossover: anti-bloat

As discussed on December 24, in some genetic programming runs we see unbounded growth of program tree sizes. This does not prevent the evolutionary optimization from running, but is inconvenient because of slower execution, potentially larger memory load, and the possibly of reducing the power of crossover the make useful changes. (Since finding the “right” place for crossover is harder in a large program).

This LimitHue::comparison() run was made with a prototype change to the crossover code. Previously a parameter to the construction of a Population has been “maximum tree size” for the initial random GpTrees. The new approach is to have a corresponding parameter for the “maximum desired tree size” for crossover during the run. If the “recipient parent” in a crossover operation has a size greater than this threshold, the crossover operation will choose the recipient subtree to be smaller than the donor subtree. As a result, the new offspring GpTree will be smaller (or in certain edge cases, the same size) than the recipient parent. As a result, the Population is generally constrained to be composed of GpTrees that (generally) are smaller than the original “maximum desired tree size” parameter.

In the current prototype implementation, this crossover limit is 1.5 times the initial limit on random tree sizes. I will probably provide API to set it directly. It also would make sense to provide API for the corresponding minimum size limit for crossover. This would mean that if the “recipient parent” were too small, the crossover subtrees would be chosen to increase the size of the offspring. I am not sure if this is ever useful, but it seems like adding it now is better than waiting to see.

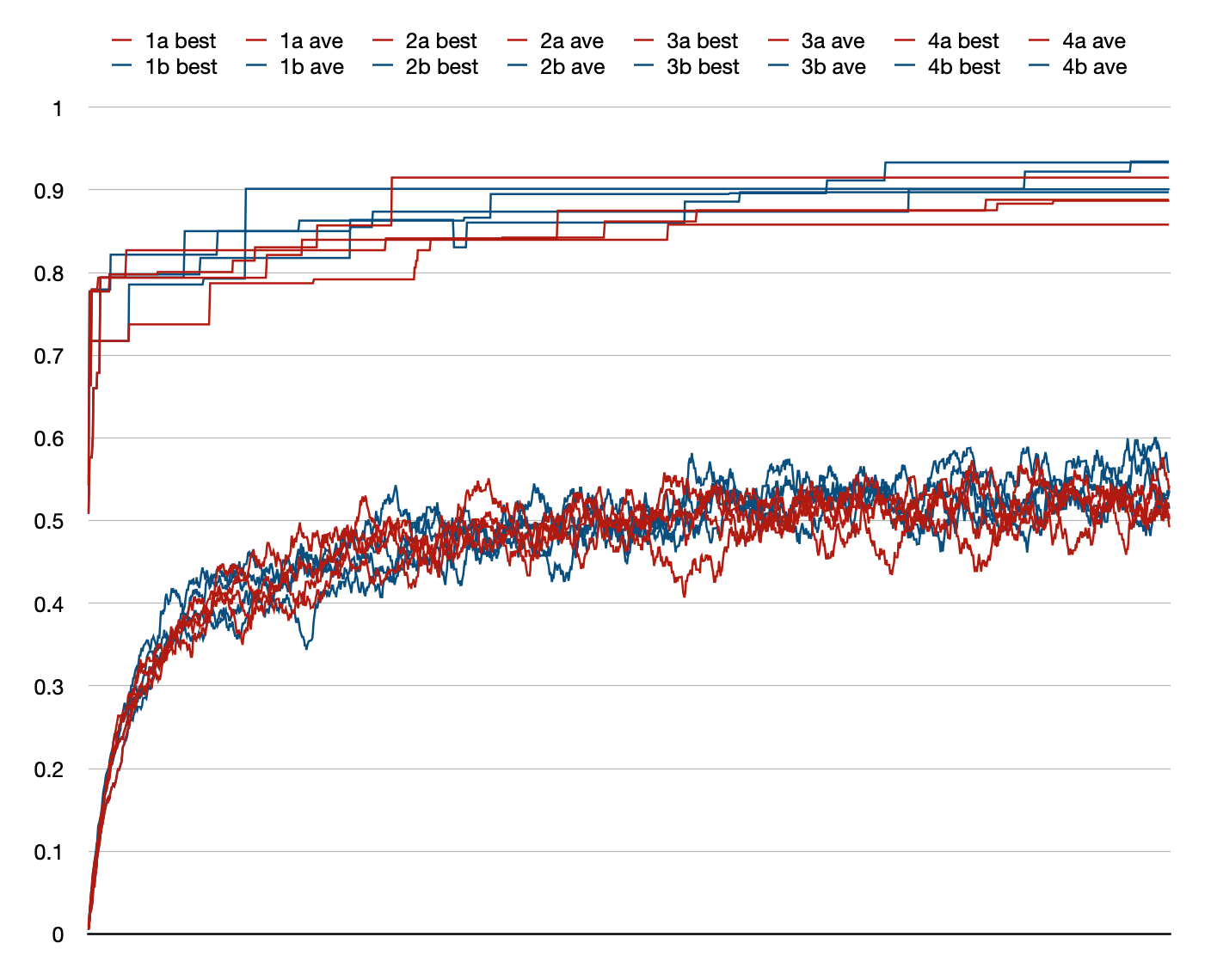
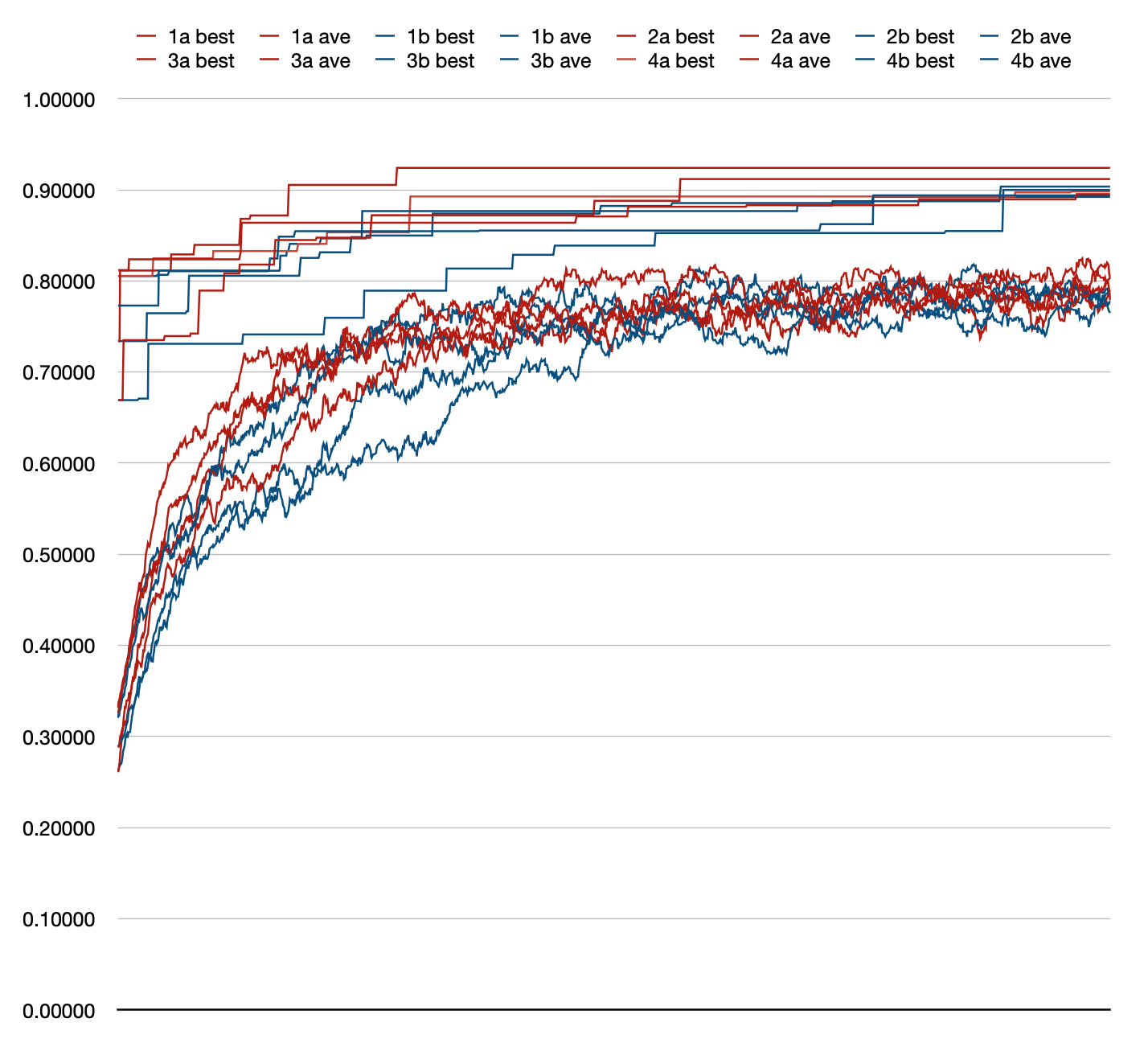
While I do not want to read too much into an experiment with n=8 but it appears in this run that the four run with the crossover size limitation (blue) have “best” and “average” fitness slightly higher than the control case without the limit (red):

In this plot of GpTree program size averaged over all in a Population, we see a clear difference between the four runs with the crossover size limit (orange) and the control runs without the crossover size limit (green). With the limit, all four runs maintain average sizes below the limit of 150 while the four runs without the limit reach size averages above 150 with one reaching about 280:

January 5, 2021

Another day, another tweak, another ambiguous plot

I changed the choice of which subpopulation is selected on each update step. It had been a random selection, now it simply rotates through them in order. Probably no difference for large runs, but in short test of 100 steps, I saw one (of four) get about 30% of the updates. I also tested the migration policy and added some other unit tests. This test is not obviously different from the previous one, although one of the 4 subpopulation runs got up to 95% which I think is the highest value I have seen. On the other hand, runs with 4 subpopulations ended at 87.6%. Like the comparison run on January 3, it is hard to see any difference in performance between using 1 (red) or 4 (blue) subpopulations.

January 3, 2021

GP with subpopulations — “demes”

For a while now subpopulations had been on my to-do list of features. This is the idea that instead of a population with, say, 100 individuals, we divide them into four subpopulations of 25 individuals each. The evolutionary computation proceeds pretty much the same as before, except that each Population::evolutionStep() starts by selecting one of the subpopulations at random. Then as before, it selects three individuals from that subpopulation, ranks them by tournament, the two top ranked individuals produce an offspring, which replaces the lowest ranked individual in the subpopulation. In addition, individuals occasionally migrate between subpopulations.

The notion is that running multiple populations in parallel allows each of them to climb a different hill in fitness space, allowing the population spread out its investment. Some of those hills might be higher than others, so multiple populations allows exploring more territory. Subpopulations are sometimes called “demes” (“from the Greek” as James Rice, my early GP mentor, told me when I asked about the term) as used in biology “ a subdivision of a population consisting of closely related plants, animals, or people, typically breeding mainly within the group.” Similarly a single population GP, as LazyPredator had been before now, is sometimes called “panmixia” from biology meaning “random mating within a breeding population.”

I refactored Population to support subpopulation and took it out for a test drive. I used the same LimitHue::comparison() framework as before, making four pairs of runs, each run in a pair starting from the same random seed, one run with a single population, and one run with four subpopulations. Each run takes 2000 steps. I hoped for a clear fitness advantage for the multiple subpopulation case. I did not find it. This plot is an excellent illustration of the null hypothesis. The plots in red have a single large population, those in blue have four subpopulations ¼ as large. It would be hard to guess which was which if they were not colored. Also puzzling is that the average fitness for all eight populations are around 0.55 while in previous runs they were near 0.75.

December 26, 2020

Oops, now computing initial “absolute fitness”

I had noticed, in TexSyn's prototype GUI, that right at the start of a run, some of the “top ten” fitness textures listed fitness of zero, which seemed incorrect. (That is, it “looked like” they ought to have higher fitness.) I first assumed this was just a bug in the GUI, but looking closer, it seemed to be a real bug. In the original tournament-based relative fitness approach, a relative fitness ranking is determined each evolution step (Population update) for the three randomly chosen Individuals. This was not happening for the later prototype absolute fitness.

The runs plotted below are like those on December 23 but an initial pass is made over the Population computing initial fitness for all Individuals. It may be just random variation between runs, but it looks like there is now generally less variance between runs, and that the best of the best are a bit higher. The overall best is 0.924 in run 3a.

I will fold this change into refactoring absolute fitness to be a layer on top of tournament-based relative fitness.

December 24, 2020 🎄

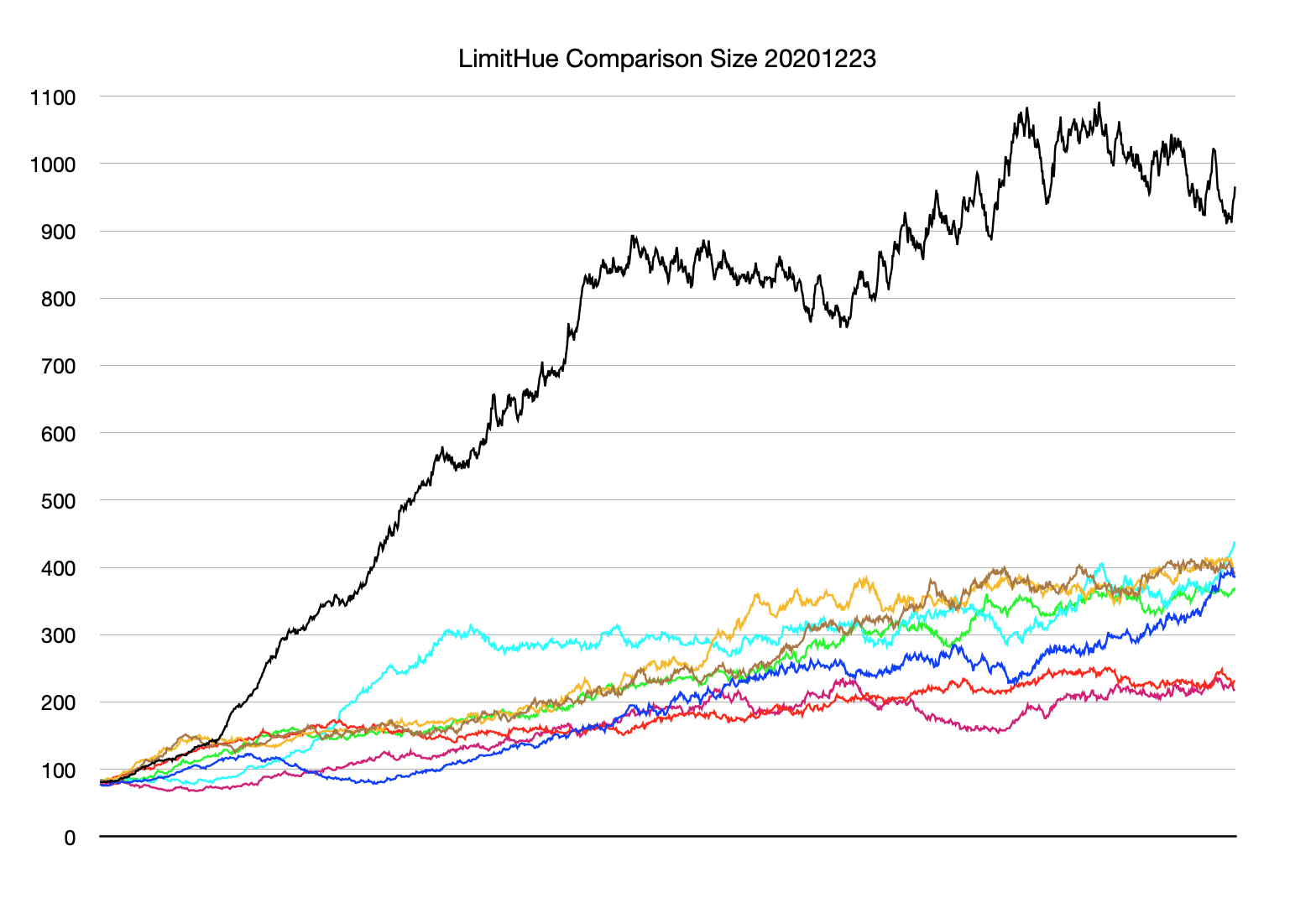
Tree size and bloat

Speaking of data from those LimitHue::comparison() runs, I also recorded average-of-population tree size for each evolution step. Recall each run was initialized with 100 individuals, each with a maximum initial tree size of 100.

(Tree size is equivalent to the number of function names and constant leaf values in the corresponding textual program notation. An interesting tidbit is that all runs start with an average tree size very close to 80. This ratio between average and maximum tree size (e.g. 80/100) probably depends on the FunctionSet being used.)

Most of the average-of-population sizes seem to end up between 200 and 400. While the first of these eight runs—the black trace in this plot—wandered into the land of giant trees, peaking up near size 1100. This occasional misbehavior of GP systems is called bloat. Tree size does not directly correlate with execution time, via GpTree::eval(), since some GpFunctions may run slower than others. But it is a safe bet that, in general, a big tree will be slower than a small tree. Larger programs certainly take up more memory, but in my applications that is not a issue. There is also a theory, a GP “folk belief”, that large trees can dilute the effectiveness of crossover.

I have a design sketched out that I hope will allow controlling tree size to avoid bloat in what I think is a fairly natural way that will not interfere with fitness measurement.

December 23, 2020

Redefine “absolute fitness” on top of relative tournaments

As discussed in the TexSyn blog on November 18, I went off on a side quest related to “absolute” fitness. This is the more common way of thinking about evolutionary computation, where an individual is tested or rated according to a fitness function, resulting in a numeric value. The goal of the optimization is then to maximize this fitness (or minimize, if you consider it an error or loss metric). LazyPredator is meant to deal primarily with “relative” fitness, as determined by competitive tournaments. (Recall the analogy: while speculative ratings can be assigned a priori to (say) athletes, it is not until they compete in a tournament that a winner is actually determined.)

However, based on what seemed like lackluster optimization based on tournaments, as a basis of comparison, I set off to re-implement the traditional evolutionary optimization, as I had done in earlier work. So instead of using tournament-based contests, I added a parallel facility for absolute numeric fitness, judging Individuals in isolation. The tournament-based evolution step looked like:

• Randomly select (with uniform distribution) three Individuals from the Population.
• Place them in a competitive tournament to produce a fitness ranking.
• The first and second place finishers are selected as “parents.”
• Use crossover and mutation to produce a new “offspring” from the parents.
• The third place finisher is removed from the population (“dies”) and replaced with the offspring.

The more traditional “absolute fitness” based evolution step was:

• Randomly select two parents from the population biased toward high fitness.
• This was done by making a uniform selection of three individuals then choosing the one with highest fitness.
• Randomly select one individual from the population, biased toward low fitness, to be replaced by the new offspring.
• This was done by making a uniform selection of three individuals then choosing the one with lowest fitness.
• Use crossover and mutation to produce a new “offspring” from the parents.
• Replace the low fitness individual with the new offspring.

Note that absolute fitness for a given individual does not change, so is computed one per individual then cached. This is generally not the case for competitive fitness.

I got to thinking about the selection procedure. In the absolute case, nine individuals are selected then used as bias to winnow down to the three actually used in the update step. I wondered if this level of “elitism” was good or bad. Parents would always be selected from the top ranked individuals in the population, because the best-of-three selection is strongly biased toward them. Conversely, all the “deaths” would be among the the very low ranked individuals. This sort of elitism may cause the evolutionary optimization to be “greedy” — to concentrate on low hanging fruit — and perhaps be short-sighted.

So I considered a different selection procedure: uniformly select three, rank those as in the competitive tournament case, the top two are the parents, and the “loser” is replaced by the new offspring. That is, the absolute fitness case is implemented as a simplistic tournament where rankings are just sorting by fitness. Unlike the nine-way selection, it is possible that all three participants (two parents, and loser) could be from the very bottom, or the very top, of the rankings. 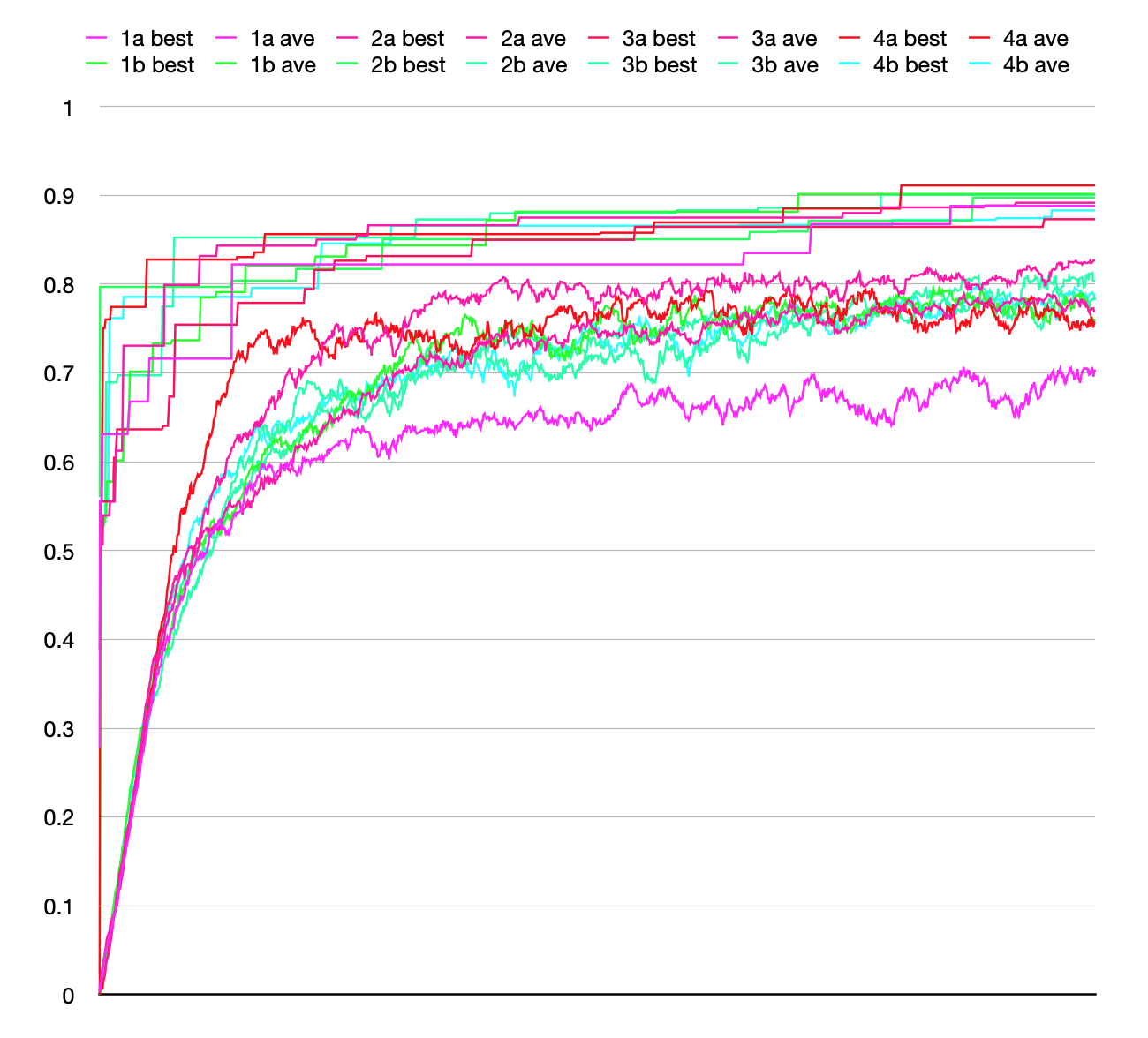I set up a comparison framework to run four rounds of both conditions (both beginning from the same random seed). Each Population consisted of 100 Individuals, each with a maximum initial size of 100. Each optimization was for for 2000 steps (which is 20 “generation equivalents”). The entire comparison of eight runs took abut 5.5 hours.

For each run, I recorded the fitness as best-of-population and average-of-population, for each of the 2000 steps. These are shown in the plot below. There are 16 lines, best and average for each of eight runs. They are color coded by condition: (a) the nine-way selection with stronger bias are in the magenta-to-red range, (b) the three-way selection with less bias are in the green-to-cyan range. The “best” at the top are monotone increasing steps, the “ave” plots are lower and noisy.

After all that, what I see in the plot is no obvious difference in performance between the a/red runs and the b/green runs. The best-of-population fitnesses end up around 0.85 to 0.90, with the averages around 0.75.  The averages of the b/green runs are closer together, possibly indicating less variance, but that is just a supposition.

I will take all this as evidence that LazyPredator's support for “absolute fitness” should be refactored to be based on top of tournament-style evolution steps.

November 27, 2020 🍗

GpTree with “phantom limb”

Toward the end of November I was tracking down a memory leak. As described here, the leak was actually in OpenCV. It took me a while to track that down because of an unrelated “confounding bug” in TexSyn's FunctionSet defined in GP.h. The actual code, a GpFunction initializer, is shown here, with the bug in red:

...
{
    "CotsMap",
    "Texture",
    {"Vec2", "Vec2", "Vec2", "Vec2", "Texture", "Texture"},
    evalTexture(CotsMap(argVec2(),
                        argVec2(),
                        argVec2(),
                        argVec2(),
                        argTexture()))
}
...

The problem is that the third line has a typo, an extra GpType specification for a Texture. It is saying that the GpFunction for CotsMap has six parameters: four of GpType Vec2 and two of Texture. In fact, as seen in the next line, CotsMap actually has five parameters, four Vec2 and one Texture. The result of this specification mismatch is that any occurrence of CotsMap in a GpTree would generate six subtrees. One of them would be ignored, specifically by GpTree::eval(), leading to uninitialized values, which caused an error in the destructor. This mismatch caused no end of confusion, especially appearing as it did during my hunt for the memory leak.

To avoid this confusion in the future I need a way to validate that these two different ways of specifying the parameters to a GpFunction match. One side has to do with actual C++ code definitions and one has to do with the abstractions used by FunctionSet. The lack of “introspection” in C++ makes this difficult. For example it would be straightforward in Lisp.

October 31, 2020 🎃

Progress report: TournamentGroup and bug fix

I have been working along, making incremental progress. After the “yellow/green” test described on October 19 I started on a slightly more ambitious test case I called “colorful, well exposed” textures (in a package named CWE). It is nearly random evolution, constrained only by tournament-based “fitness” tests that favor textures with a full range of brightness (luminance) and color saturations. It measures these by uniformly sampling colors from the texture, placing them into a histogram (of saturation or brightness) then scoring the histogram's flatness (uniformity).

Previously, a lot of my prototype tournament functions had the structure of passing in three Individual* pointers and returning the “worst” one, the loser of the tournament. This felt awkward and led to duplicated code (e.g. for finding best or worst individuals). So I refactored things to put most of that into a new class TournamentGroup. It encapsulates the previously duplicated code and serves as a container for the individuals in a tournament, with the side benefit of allowing them to have arbitrary size. (In case there is ever a need for tournaments with 2 or 10 participants.) Always the careful incrementalist, I made an #ifdef flag so converting to using the new class was reversible. I got the CWE test running with TournamentGroup then went back to verify I got the same result from the old and new code. I did not. While poking around I realized that the old code had a significant bug in Population::evolutionStep(). It was related to that “duplicated code” issue, and was definitely doing the wrong thing in ⅓ of the cases.

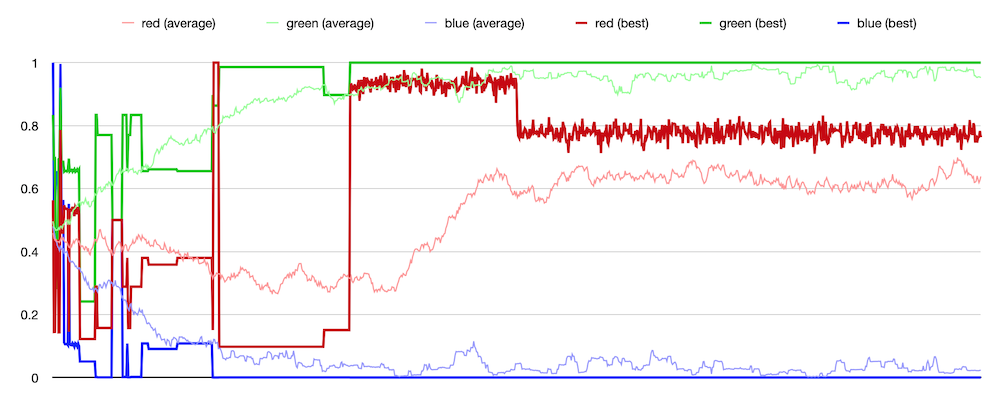
After various testing, I went back to the YG (“yellow/green”) test and reran it, using the new TournamentGroup-based bug-free code and got much more satisfying results. The October 19 results seemed disappointingly “indecisive.” I had expected the green level to push right up toward 100% and the blue level to drop down near zero. Instead the results less convincing—green was highest, red in the middle, and blue lowest—but they wandered in the mid-range instead of pushing out to the bounds. I plotted the results of the new run and it looked much better. Not only are the “population best” green/blue values very close to the bounds, but the “population average” are within about 5% of the bounds. Also this run is 1000 evolution steps long. The run on October 19 was five times longer and never got this close to its goal.

October 19, 2020

Evolution: first quantitative data

I did some more tooling work, and collected some data on the simple test application I described on October 17. As then, there are 3-way tournaments. Three TexSyn textures compete based on their “average color.” That is, as if they were infinitely blurred, and could be represented by a single color in RGB space. The tournaments have two cases, one of which is selected randomly. The three textures compete for either (a) the highest green component of their three average colors, or (b) the lowest blue component. This should drive the population toward colors with high green, low blue, and unconstrained red. This describes colors in the yellow-to-green region.

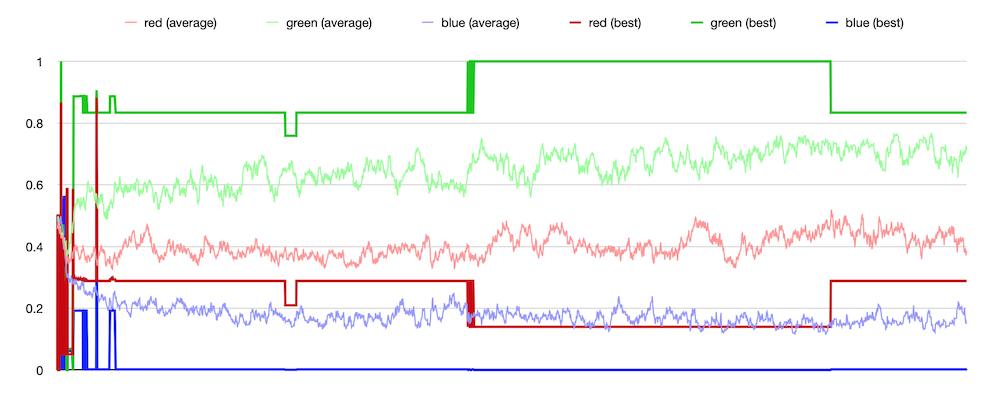
The run plotted below has a population size of 50, and was run for 5000 steps (which corresponds to 100 “generation equivalents”). This took about 20 minutes, or longer if I rendered the textures. Originally I displayed them one after another, as sort of a flickering movie, which allowed me to see they were trending toward yellow/green color schemes. I recorded ad hoc data and made some plots. I looked at the “average average” color—taking the average color of all 50 textures in the population and averaging them together each step. That produces the wiggly lines in the plot below identified in the legend as “red (average)” etc. This looked OK, the green was higher, blue lower, and red seemed to drift someone in between. Then I selected one member of the population as “best.” This is subject to change. My current criteria for “best” is the member of the population which has “survived” the most tournaments. Since losing a tournament (being ranked third of three) leads to an individual being removed from the population, it seems that the number of times one has been tested and survived is some proxy of quality. The three step-like plots show this current “best” individual's average red, green and blue. The step changes are when a new best comes along, then holds steady until the next change of rankings. Unlike the “average average” plots, these “best” values are closer to the extremes, near or at the bounds of unit RGB space. (TexSyn does not place bounds on color values, but I used Color::clipToUnitRGB() when computing average colors for this run.)

One unrelated problem that arose during this work had to do with “minimum size for crossover snippet” as discussed on October 8. On a whim I had chosen a value of five, while the smallest valid TexSyn tree has size four, as in: Uniform(0.3, 0.8, 0.4). My thought was I would rather see slightly larger subtrees used for crossover. It seemed to work fine until today when I was initializing a larger population of size 50. One of those initial random trees just happened to be that minimal size four example.That led to an obscure divide by zero error. I made a temp fix but it needs some more thought.

October 18, 2020

Fixing that mutation problem, setting jiggle scale.

I re-enabled GpTree::mutate() and tracked down the problem seen earlier. The added-in-a-hurry GpType::getMaxJiggleFactor() function was misbehaving (the wrong this pointer was captured in the jiggle handler lambda). The intent was to allow customizing the “jiggle scale” but as I had noted in the code, it was not obvious how or when that could happen. I suspect it does not really matter. The default value (of up to ±5% of the given numeric range of a GpType) would probably be fine. But if some imaginary future user of LazyPredator did need to tweak that value they would be annoyed it was not settable.

So instead, the mutation bug is now fixed, and the “jiggle scale” still defaults to 0.05 via a new static function called GpType::defaultJiggleScale(), but can be overridden by yet another constructor for the class. For example one of the TexSyn GpTypes is currently written:

...
{ "Float_01", 0.0f, 1.0f },
...

with its “jiggle scale” defaulting to ±5%, or a custom value can be given like this:

...
{ "Float_01", 0.0f, 1.0f, 0.2f },
...

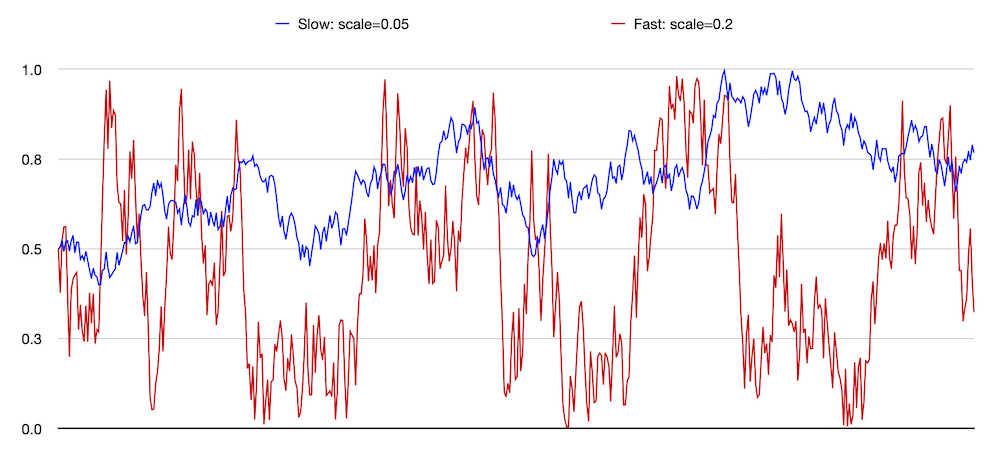
indicating the jiggle scale for that type is ±20% of the given range [0, 1]. Shown below is a plot of repeated jiggle mutations of values from two such GpType definitions. The blue trace corresponds to the default jiggle scale of 0.05 and the red trace with a scale of 0.2. The red trace can change by four times the amount of the blue trace—per mutation—so moves four times faster. There are 500 steps across the horizontal axis.

October 17, 2020

Evolution, almost certainly!

Huzzah! On October 15 I cobbled together a minimal evolution run, using the TexSyn API. I ran a small number of “steps” — steady state population updates — and it did not crash. The next day I cleaned up the prototype tournament function so it might actually be correct. Then I tried a longer run. I got to step 61 when it failed an assert (in TexSyn's RGB↔︎HSV conversions). That code has been stable for many months, as I dug in it seemed to just be noticing bad input data (floating point nans). Then followed a lot of unsuccessful attempts to isolate the failure. Finally I recalled that I had slapped together GpTree::mutate() just before trying an evolution run. Indeed, when I commented out the call to that, the assert failures stopped. To be fixed soon.

Even better, when I let my tiny Population of 10 Individuals run for 1000 steps — what my non-steady-state peeps would call “100 generations” — the Population seemed to be clearly evolving toward the goal state. As mentioned in the previous post, I was looking only the “average color” of the TexSyn Texture which is the value of the evolving Individuals. In fact, I looked only at the green and blue components of the average color (in RGB space) so all details of textures are ignored. The “winners” of a tournament among three Textures are the two whose average color have either: the higher green level, or the lower blue level. (Conversely: the “loser” of the tournament is the color with the lowest green or highest blue.) This is a simplistic example of a 3-way tournament and multi-objective optimization. Participants in the tournament are chosen at random, uniformly across the Population. The tournament then makes a uniform random choice between minimizing blue or maximizing green. As the 1000 step evolution ran, the tournament-winning texture clearly moved into the green-to-yellow color range. (The red RGB component is ignored, so allows drift across the green-yellow range.)

There is lots more to do, but at least LazyPredator has passed into “not obviously broken” territory. I noticed that the modest 1000 step run accumulated 1.8 GB of memory which means it's leaking memory like mad. OpenCV Mat objects are a likely candidate.

October 15, 2020

Evolution, maybe?

I think I got all the pieces glued together sufficiently so this afternoon I was able to “turn the crank” on an evolutionary computation, if only briefly. It is at least running. Not sure if it is actually working. The first version was using random tournaments, so it was impossible to tell. Then I tried to make a simplistic tournament function. Using the TexSyn FunctionSet, I told it to prefer textures whose average color had high levels of green or low levels of blue. This should produce textures which are primarily in the green-to-yellow neighborhood of color space. Again, it ran OK, but no obvious evolutionary change in such a short test.

October 14, 2020

Back to Population and Individual

After about two months developing a representation for genetic programming (FunctionSet, GpTree, GpFunction, and GpType) I have returned to the basics of evolutionary computation: Individual and Population. My initial plan is to avoid the traditional numeric measure of fitness, instead using relative fitness as measured in competitive tournaments. For some definitions of fitness, there is no significant difference. If we define the fitness of a tower as its height, then that one number tells us all we need to know about an individual. But in other kinds of fitness—for example, which team in a sports league is best—all that can be established is a relative ranking. We cannot evaluate a team to produce a single numeric fitness that predicts which of two teams will win a match.

My initial plan is to use tournaments of three Individuals from the Population. This provides a minimalist replacement strategy for the “steady state genetic algorithm”: three individuals are selected at random (neutral selection, not “fitness proportionate”), they compete in a three-way contest, the Individual which does the worst is removed from the Population, and replaced with a new offspring, formed by crossover between the other two Individuals in the tournament. It is not required to establish a “full ordering” of the three Individuals, only to determine which is in last place. The ranking of the other two is ignored.

Yesterday I experimented with several implementations of Population::selectThreeIndices() to select three random but unique (“without replacement”?) members of the population to be in a tournament. (The “modern c++17 way” of doing this is with std::sample() but for the moment I needed to use LP's RandomSequence API.) Today I started building out the Individual and Population classes. I am now able to initialize a Population of a given size, where each Individual is initialized with random GpTree of a given max size from a given FunctionSet.

October 11, 2020

“Jiggle” mutation for numeric leaf values.

Based on yesterday's streamlining for ranged numeric types, it was pretty easy to add a new handler function to GpType to provide “jiggle” mutation for the numeric constant values found at leaves of GpTrees. Like yesterday, I only supported c++ concrete types int and float. If others are needed they can be added later, or explicitly implemented using the older, more general form of GpType constructor. The jiggle handler function is automatically constructed for a ranged numeric GpType, based on the given range bounds and a parameter prototyped as GpType::getMaxJiggleFactor(). 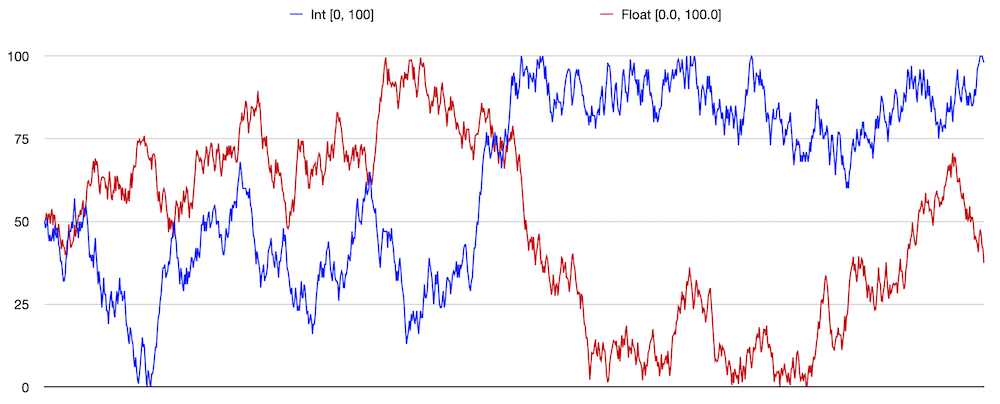It is currently set to 0.05 so at any given jiggle, a value will be offset by up to ±5% of the given range. Here is a little test code to watch iterated jiggle of an int and float type on the range [0, 100]:

GpType ti("Int", 0, 100);
GpType tf("Float", 0.0f, 100.0f);
std::any vi = 50;
std::any vf = 50.0f;
for (int k = 0; k < 1000; k++)
{
    vi = ti.jiggleConstant(vi);
    vf = tf.jiggleConstant(vf);
    std::cout << ti.to_string(vi) << ", ";
    std::cout << tf.to_string(vf) << std::endl;
}

The result behaves as a “bounded Brownian” series. It stays within the given range, covering the entire range, while not hugging the bounds due to clipping. I took the log from that code and pasted it into a speadsheet for plotting:

October 10, 2020

GpType constructors: less is more

Two key operators in genetic programming are crossover and mutation. Crossover has been discussed before. I was starting to think about a “point mutation” operator on GpTrees that adds noise to numeric parameters in a tree's leaves. This is not about that, but was prompted by setting the stage for it. The definition of TexSyn's FunctionSet consists of two collection: GpTypes and GpFunctions. (And now a third parameter for crossover_min_size.) Before today, the GpType specs looked like this:

{
    { "Texture" },
    { "Vec2" },
    {
        "Float_01",
        [](){ return std::any(LPRS().frandom01()); },
        any_to_string<float>
    },
    {
        "Float_02",
        [](){ return std::any(LPRS().frandom2(0, 2)); },
        any_to_string<float>
    },
    {
        "Float_0_10",
        [](){ return std::any(LPRS().frandom2(0, 10)); },
        any_to_string<float>
    },
    {
        "Float_m5p5",
        [](){ return std::any(LPRS().frandom2(-5, 5)); },
        any_to_string<float>
    }
}

I have been glossing over this format for GpType constructors, since it felt a little preliminary. Texture and Vec2 are used only as tags to correctly matching up inputs and outputs of GpFunctions. The other four types are specializations of the concrete c++ type float. These four types differ only in the range of values they represent. For example, Float_01 are values on the interval [0.0, 1.0] and Float_m5p5 are values on the interval [-5.0, 5.0]. For each GpType “initializer list” (between braces {}) there is: (1) a character string name, (2) a function to return a random “ephemeral constant” uniformly selected from the type's range, and (3) a function that casts from a value of this type to a character string for printing. (The values actually passed around are of type std::any for “type erasure” but let's not get into that right now.)

I came up with a way to make this less messy. I hope eventually that LazyPredator will be used for other applications. For now however, it is only being used with the FunctionSet for TexSyn. So this may be short-sighted, but so far, a GpType either just tags an instance of a c++ class (like Texture and Vec2) or it represents a numeric type, perhaps with range constraints (like Float_01 ... Float_m5p5). So rather than writing out the two (soon to be three) handler functions/lambdas, all we need to specify are the ranges. I defined two new constructors for GpType one for float and one for int that takes: a name, range_min, and range_max. The internal structure of a GpType object is unchanged, this is just a different way to initialize its internal state. The result is a much more compact specification for the GpTypes of a FunctionSet:

{
    { "Texture" },
    { "Vec2" },
    { "Float_01", 0.0f, 1.0f },
    { "Float_02", 0.0f, 2.0f },
    { "Float_0_10", 0.0f, 10.0f },
    { "Float_m5p5", -5.0f, 5.0f }
}

I like this approach. The connection with mutation operators is that soon there would have been need for a fourth item in GpType's initializer list: a function to “jiggle” an existing value of this type. Having defined a GpType as a ranged numeric value, we can automatically generate the handlers for randomizing, printing, and soon, for mutating. The older constructors remain available for cases not covered by this streamlining.

October 8, 2020

Minimum size for crossover snippet

I am developing LazyPredator and TexSyn in parallel, so sometimes its hard to decide which “blog” should get a post. Recent work with GP crossover was been reported in TexSyn's posts on October 3 and October 5 (and previously on this page on September 30). The topic of the October 5 post, and this one, is the question of whether random “crossover points” in a pair of parent GP trees should be selected uniformly across all nodes in the trees. I think this is the most common and “traditional” approach. But I decided to allow a variation on this which seems useful in a concrete case like TexSyn's FunctionSet.

The GP tree crossover operation is based on selecting, in two “parent” trees, a pair of nodes. Those two nodes are the roots of two subtrees, which can be thought of as a snippet of code in normal linear textual code notation. We copy the selected subtree of the “donor” tree, and paste it over the subtree of the “recipient”/offspring tree.

But let's back up a bit, how is the random selection of a node in each tree defined? In the October 3 examples this was done in what I consider the “traditional” way: a recursive traversal of the tree is made and a reference to each node/subtree is stored in an array (in this case an std::vector), then a random index over the size of the array is generated and the corresponding subtree is selected. (Equivalently without the array: one traversal measures the size of the tree, the random index is determined, then a second traversal is made until it reaches the node corresponding to that index, which is returned.) This means that the selection of tree nodes is uniformly distributed over all nodes in the tree.

Because LazyPredator is based on STGP (strongly typed genetic programming) there is an additional constraint that the two selected subtrees have the same type (GpType). This is accomplished by first selecting a node in the “donor” tree, then filtering the nodes of the “recipient” tree to consider only subtrees with a matching type.

Consider this (partially redacted) FunctionSet. It shares a property with TexSyn that the root type (Thing) has no “ephemeral constants”, while the other type (Int) has no operators, appearing only as numeric constant leaf nodes:

FunctionSet fs =
{
    // GpTypes:
    {
        {
            "Thing", nullptr, any_to_string<...>
        },
        {
            "Int", [](){ return std::any(int(LPRS().randomN(10))); }, any_to_string<int>
        }
    },
    // GpFunctions:
    {
        {
            "This", "Thing", {"Thing", "Thing"}, [](const GpTree& t) { ... }
        },
        {
            "That", "Thing", {"Thing", "Thing"}, ](const GpTree& t) { ... }
        },
        {
            "Other", "Thing", {"Int", "Int"}, [](const GpTree& t) { ... }
        }
    }
};

This is a typical random GpTree, of size 55, created by that FunctionSet with 28 numeric constant leaf nodes (in red):

This(Other(9, 0),
     That(This(This(This(Other(8, 2),
                         This(Other(5, 9),
                              Other(3, 8))),
                    Other(3, 1)),
               That(This(This(Other(6, 1),
                              Other(8, 1)),
                         Other(4, 0)),
                    This(Other(3, 2),
                         That(This(Other(9, 4),
                                   Other(6, 9)),
                              This(Other(6, 4),
                                   Other(1, 9)))))),
          Other(9, 6)))

Note that 28/55 or about 51% of random nodes (selected uniformly) will be these numeric constants. So given two GpTrees from this FunctionSet, roughly half of all crossover operations will consist of moving a single numeric constant from one tree to the other. (Recall that in STGP, Ints from one tree can only crossover to Ints in the other tree.) About half the crossover operations will do nothing but parameter “tweaking” and in a way that ignores the context that would normally exist when a larger subtree is moved. I would prefer that “tweaking” constant leaf values be done by point mutation, which is defined to make “small” changes in value.

Consider instead this version of that FunctionSet, identical but with the new crossover_min_size parameter added at the bottom:

FunctionSet fs =
{
    // GpTypes:
    {
        ...
    },
    // GpFunctions:
    {
        ...
    },
    // Min_size for crossover:
    2
};

By increasing the crossover_min_size to 2 from its default of 1, this requires that all crossover subtrees/snippets must be of size 2 or larger. Specifically this means that a single numeric constant leaf value (of size 1) is excluded from selection as the crossover subtree/snippet. (As mentioned above, this is accomplished by filtering the set of candidate subtrees, in this case by size.) The effect of this is that all crossover snippets must consist of subtrees larger than a single leaf node. In terms of the random program above: all of the red leaf nodes are excluded, and the selection must be one of the larger subtrees in black. In the examples shown in TexSyn's blog for October 5, a crossover_min_size of 5 is used, implying that the crossover snippet must be larger than the minimal (size 4) Texture generator of Uniform(r, g, b), a “texture” of uniform color.

September 30, 2020

Crossover of GpTrees — wait, that was too easy

In biology chromosomal crossover is a key mechanism where the DNA of two parents is combined to produce a unique offspring. Two corresponding strands of parental DNA are “scanned” in parallel, with one or the other being copied into the new offspring's DNA. During this “scan” the source of the offspring's DNA changes “randomly” from one parent to the other. (If you are a biologist, please forgive this over-simplified probably incorrect description.)

In genetic programming there is an analogous “crossover” operation on program trees. When describing GP I often call this “random syntax-aware copy-and-paste.” It is as if a subtree (subexpression) from one parent's program is copied, then pasted into (a copy of) the other parent's program, replacing a preexisting subtree (subexpression). This creates a new offspring program with part of its code from one parent and part of its code from the other parent. LazyPredator implements “strongly typed genetic programming” so there is the additional constraint that the type of the two subtrees must match. (In TexSyn, most of the subtrees are of type Texture, but some subtrees return Vec2 or numeric float values.)

Crossover had been on the to-do list for a while and I finally got around to working on it. I defined a new test FunctionSet whose terminals are all single digit integers, and whose functions belong to two families: P, PP, PPP, Q, QQ, and QQQ. Here is that FunctionSet's self description:

1 GpTypes: 
GpType: Int, min size to terminate: 1, has ephemeral generator, has to_string, functions returning this type: P, PP, PPP, Q, QQ, QQQ.

6 GpFunctions: 
GpFunction: P, return_type: Int, parameters: (Int).
GpFunction: PP, return_type: Int, parameters: (Int, Int).
GpFunction: PPP, return_type: Int, parameters: (Int, Int, Int).
GpFunction: Q, return_type: Int, parameters: (Int).
GpFunction: QQ, return_type: Int, parameters: (Int, Int).
GpFunction: QQQ, return_type: Int, parameters: (Int, Int, Int).

I also added a mechanism to FunctionSet allowing a filter to be specified on the available functions. Here are randomly created program trees drawn from the two sets:

// makeRandomTree() called with function filter allowing only the P family:
PPP(PPP(P(7), P(P(1)), PP(4, 3)), P(PPP(P(8), P(P(0)), PP(8, 4))), PPP(P(P(1)), P(P(6)), P(P(7))))

// makeRandomTree() called with function filter allowing only the Q family:
QQQ(Q(QQQ(Q(7), Q(2), QQ(5, 8))), Q(QQQ(Q(5), QQ(5, 3), Q(Q(3)))), QQQ(QQ(3, 4), QQ(6, 1), QQ(8, 1)))

Then I manually selected a subtree from each of those GpTrees:

// gp_tree_p.getSubtree(0):
PPP(P(7), P(P(1)), PP(4, 3))

// gp_tree_q.getSubtree(2):
QQQ(QQ(3, 4), QQ(6, 1), QQ(8, 1))

Then I assigned one to the other:

gp_tree_p.getSubtree(0) = gp_tree_q.getSubtree(2);

Et voila!:

PPP(QQQ(QQ(3, 4), QQ(6, 1), QQ(8, 1)), P(PPP(P(8), P(P(0)), PP(8, 4))), PPP(P(P(1)), P(P(6)), P(P(7))))

Writing that again with indentation and color to highlight the subtrees:

// The P tree with it first subtree selected:
PPP(PPP(P(7), P(P(1)), PP(4, 3)),
    P(PPP(P(8), P(P(0)), PP(8, 4))),
    PPP(P(P(1)), P(P(6)), P(P(7))))

// The Q tree with it third subtree selected:
QQQ(Q(QQQ(Q(7), Q(2), QQ(5, 8))),
    Q(QQQ(Q(5), QQ(5, 3), Q(Q(3)))),
    QQQ(QQ(3, 4), QQ(6, 1), QQ(8, 1)))

// The offspring tree with some of both:
PPP(QQQ(QQ(3, 4), QQ(6, 1), QQ(8, 1)),
    P(PPP(P(8), P(P(0)), PP(8, 4))),
    PPP(P(P(1)), P(P(6)), P(P(7))))

September 21, 2020

Runtime connection between LazyPredator and TexSyn

[Update on September 29, 2020: after some further revisions, I made a “first final” FunctionSet for TexSyn. The code below is both incomplete and slightly outdated. To see the “modern” FunctionSet for TexSyn in this source code: GP.h (assuming I did that right, it should be a permalink to the revision of GP.h as of September 29 on GitHub.)]

Finally LazyPredator and TexSyn are talking together at runtime! I had mocked this up back on August 15 by having prototype FunctionSet:makeRandomTree() print out the “source code” of generated trees, then hand editing that into a test jig in TexSyn and rendering the textures. Now it is actually working, directly evaluating the GpTree and then passing that result to TexSyn's render utility. See renderings in today's the TexSyn log.

I was not looking forward to the software engineering of making LazyPredator into a proper linkable library. Instead I took the path that is becoming more popular, especially for libraries of modest size like LazyPredator: I made it a header-only library. Then “linking” it to TexSyn was merely a matter of adding the directive #include "LazyPredator.h".

I wrote a subset of the FunctionSet definition for TexSyn (similar to an earlier prototype in LP called TestFS::tinyTexSyn()) for testing. It supports GpTypes for Texture pointers, Vec2 values, and Float_01 values. It provides two GpFunctions as Texture operators : Uniform and Spot:

const FunctionSet tiny_texsyn =
{
    {
        {"Texture"},
        {"Vec2"},
        {
            "Float_01",
            [](){ return std::any(LPRS().frandom01()); },
            any_to_string<float>
        }
    },
    {
        {
            "Vec2",
            "Vec2",
            {"Float_01", "Float_01"},
            [](const GpTree& tree)
            {
                return std::any(Vec2(tree.evalSubtree<float>(0),
                                     tree.evalSubtree<float>(1)));
            }
        },
        
        {
            "Uniform",
            "Texture",
            {"Float_01", "Float_01", "Float_01"},
            [](const GpTree& tree)
            {
                Texture* t = new Uniform(tree.evalSubtree<float>(0),
                                         tree.evalSubtree<float>(1),
                                         tree.evalSubtree<float>(2));
                return std::any(t);
            }
        },
        
        {
            "Spot",
            "Texture",
            {"Vec2", "Float_01", "Texture", "Float_01", "Texture"},
            [](const GpTree& tree)
            {
                Texture* t = new Spot(tree.evalSubtree<Vec2>(0),
                                      tree.evalSubtree<float>(1),
                                      *tree.evalSubtree<Texture*>(2),
                                      tree.evalSubtree<float>(3),
                                      *tree.evalSubtree<Texture*>(4));
                return std::any(t);
            }
        },
    }
};

The next step is to build these out to include the ~50 Texture operators in TexSyn.

September 19, 2020

Tweaks to FunctionSet

Well that exploded quickly! I noticed that the recording of GpType with a constant “leaf” value in a GpTree was wrong, which was going undetected, and ultimately not mattering. The latter—that the GpType is redundant since it can be inferred from the parent GpTree node—is an issue to consider later. However if the value is stored it ought to be correct. It either needed to be error checked (which it now is, at least in the unit test) or set in sync with the tree's root function or leaf value are set. I changed GpTree::setFunction() and GpTree::setLeafValue() to record a GpType in the GpTree's root.

Or that was what I did after I fixed the other bug I ran into. Sample FunctionSets are defined in TestFS. Those are immutable const references. I had been copying those because previously FunctionSet assumed it could mutate itself. So I made several changes to allow FunctionSets to remain immutable. Part of that was to move a RandomSequence object from inside FunctionSet out to global scope, now accessed as LPRS(). That also needs to be reconsidered. Maybe it should belong to Population class or something else. In any case, the point is to have restartable random number sequences when that is helpful for testing or debugging.

I was also concerned that there were four nearly identical short functions in FunctionSet: const and non-const versions of lookupGpTypeByName() and lookupGpFunctionByName(). In fact their bodies were exactly identical, the differences were const-ness of the functions and their return values. I tried making their bodies a common function, then a common template, then finally fell back to a common preprocessor macro. Not pretty, but some times you just need to turn off type checking.

Finally, since its role is to create a random GpTree, I renamed FunctionSet's makeRandomProgram() to makeRandomTree().

September 15, 2020

Tree evaluation to construct procedural models

The previous post demonstrated evaluating GP trees to produce a numeric result. This is easier when all tree nodes have numeric values (or other “plain old data” (POD) types). It is more complicated when the values in a tree represent data structures or abstractions like class instances. It is trivial to copy (say) a numeric value, but the cost of copying a composite object can be significantly higher to handle the data and procedural state of an object. (As a concrete example, during initialization, TexSyn's LotsOfSpots texture operator builds a moderate-sized data set and runs a relaxation procedure on it.) So generally, we need to be able to pass “references”/“pointers” to these larger objects in addition to copying “plain old data” types (and small instances: TexSyn routinely copies Vec2 objects whose entire state is just two floats).

LazyPredator is being built to optimize TexSyn procedural texture models. In this mode of use, GP programs are evaluated to construct a secondary representation, here a tree of TexSyn texture operator instances (plus 2d vectors and numbers). From a c++ point of view, the GP tree represents a deeply nested expression consisting of class constructors. Evaluating that expression builds the various texture operators, using the supplied parameters, some of which are themselves newly constructed texture operators. Once built these procedural texture models can be used to render the texture for display or file output, or to place the texture into evolutionary competition with other textures.

To test this capability I made a toy example (analogous to but separate from TexSyn) based on these three classes:

class ClassA
{
public:
    ClassA(const ClassB& b, ClassC c) : b_(b), c_(c) {}
    ...
private:
    const ClassB& b_;
    const ClassC c_;
};

class ClassB
{
public:
    ClassB(float f) : f_(f) {}
    ...
private:
    float f_;
};

class ClassC
{
public:
    ClassC(int i, int j) : i_(i), j_(j) {}
    ...
private:
    int i_;
    int j_;
};

Note that ClassA's first parameter is a ClassB instance passed by reference and its second parameter is a ClassC instance passed by value. The new UnitTests::gp_tree_eval_objects() uses the FunctionSet from TestFS::treeEvalObjects() to construct, then evaluate, this tree:

ClassA(ClassB(0.5), ClassC(1, 2))

It then verifies that the ClassA instance constructed is valid, contains a reference to a valid instance of ClassB and a copy of a valid ClassC instance, and all have the expected internal state.

New UnitTests::gp_tree_eval_simple() similarly tests evaluation of GpTrees with numeric values.

September 7, 2020

Evaluating program trees

Today I finally got past a roadblock which held me up for a week. The code to generate a random program was working well, and the GpTree containers were solid. But I had not yet connected my abstract GpFunctions and GpTypes to the “real world” of c++ types. This would be required to support “evaluation”/“execution” of the GpTree.

Generally in c++ when you want to parameterize something by types, you use a “template.” As I had been working along, I assumed I would derive templated versions of GpFunctions and GpTypes to accommodate the concrete c++ types. There were problems with that, chiefly that “template virtual functions” are not a thing. I tried several refactorings but none allowed me to generalize over the set of concrete types. I even considered “hiding” the types inside an abstraction where they were stored as void* / std::shared_ptr<void> pointers, with the required “casting” to concrete types on the way in and out. Of course that is not “type safe” so a bug can lead to bizarre “undefined behavior.”

While reading about that I discovered that the c++17 standard introduced a new “meta type” called std::any. It is nearly identical to the void* trick, while keeping track of the type of the data behind the blind pointer for error checking, and being fully supported by the language and compiler. Yay! So now the GpTree keeps track of values of arbitrary c++ types via type std::any. The GpTypes and GpFunctions “know” the concrete types, so provide the transformations via std::any_cast<T>(A) which casts A, an std::any, to a value of concrete type T. One consequence of this is that LazyPredator requires c++17 (whereas before, c++11 was good enough).

For a simple example, imagine a FunctionSet consisting of two types and these five functions:

Int AddInt(Int a, Int b) {…}
Float AddFloat(Float a, Float b) {…}
Int Floor(Float a) {…}
Float Sqrt(Int a) {…}
Float Mult(Float a, Int b) {…}

In the code, this is currently written like this. The FunctionSet takes a collection of GpTypes and one of GpFunctions. Each takes “helper functions” (lambdas, function pointers, callbacks) that handle casting, generating ephemeral constants and evaluating concrete functions. (So for example, AddInt is passed a reference to some node in a GpTree, it evaluates the subtrees corresponding to its parameters, casts those to concrete types, applies its own underlying function to them, and returns the result as an std::any):

FunctionSet test_tree_eval =
{
    // GpTypes (with ephemeral constant generatorss, and to_string handlers).
    {
        {
            "Int",
            [](){ return std::any(int(rand() % 10)); },
            any_to_string<int>
        },
        {
            "Float",
            [](){ return std::any(frandom01()); },
            any_to_string<float>
        }
    },
    // GpFunctions (with a lambda to apply function to parameter via a GpTree)
    {
        {
            "AddInt", "Int", {"Int", "Int"}, [](const GpTree& t)
            {
                return std::any(t.evalSubtree<int>(0) + t.evalSubtree<int>(1));
            }
        },
        {
            "AddFloat", "Float", {"Float", "Float"}, [](const GpTree& t)
            {
                return std::any(t.evalSubtree<float>(0) + t.evalSubtree<float>(1));
            }
        },
        {
            "Floor", "Int", {"Float"}, [](const GpTree& t)
            {
                return std::any(int(std::floor(t.evalSubtree<float>(0))));
            }
        },
        {
            "Sqrt", "Float", {"Int"}, [](const GpTree& t)
            {
                return std::any(float(std::sqrt(t.evalSubtree<int>(0))));
            }
        },
        {
            "Mult", "Float", {"Float", "Int"}, [](const GpTree& t)
            {
                return std::any(t.evalSubtree<float>(0) * t.evalSubtree<int>(1));
            }
        }
    }
};

Using that FunctionSet, called test_tree_eval, here is a random program of size 10, whose value is 3.60555:

Sqrt(AddInt(AddInt(6, Floor(0.262453)), AddInt(7, Floor(0.736082))))

And here is a random program of size 100, whose value is 74.2361:

AddFloat(Mult(Mult(AddFloat(AddFloat(Sqrt(4), Sqrt(0)), Sqrt(Floor(Mult(0.081061, 5)))), Floor(AddFloat(AddFloat(Sqrt(7), Sqrt(5)), Mult(Sqrt(0), Floor(0.269215))))), Floor(AddFloat(Mult(AddFloat(Sqrt(4), Sqrt(7)), Floor(AddFloat(0.776866, Sqrt(4)))), AddFloat(Sqrt(Floor(AddFloat(0.422460, 0.282156))), Sqrt(Floor(AddFloat(0.193967, 0.011316))))))), AddFloat(Sqrt(Floor(Mult(Mult(Mult(0.191824, Floor(0.983236)), Floor(AddFloat(0.244054, Sqrt(1)))), Floor(Mult(Sqrt(AddInt(8, 5)), AddInt(Floor(0.601010), Floor(0.176880))))))), AddFloat(Sqrt(AddInt(AddInt(Floor(0.828355), Floor(0.157731)), AddInt(Floor(0.987937), Floor(0.257169)))), Sqrt(Floor(AddFloat(Sqrt(Floor(Sqrt(7))), AddFloat(Sqrt(7), Sqrt(3))))))))

August 29, 2020

Progress on GpTree

A dirty little secret of FunctionSet::makeRandomProgram() was that it did not actually “make” a program. It had been just going through the motions, and printing out a textual representation of the program it would be making, if only there was an internal representation of programs. Now there is GpTree which I have been building out for a few days, adding tools for building and accessing them. A FunctionSet is defined as a grammar in terms of GpType and GpFunction. Now FunctionSet::makeRandomProgram() stores its result in a GpTree object. They have a GpTree::size() function which had previously been handled by makeRandomProgram(). Similarly GpTree::to_string() does a translation to “source code” as an std::string, mostly for debugging and logging.

The FunctionSet for TexSyn is particularly simple: all function returns Texture, except Vec2, and the only other component is float constants. I had not initially handled the case where a GpType can be supplied by either a “leaf” constant or a subtree of functions. So I defined a little FunctionSet that had that issue:

FunctionSet fs = {
                     {
                         {"Int", [](){ return rand() % 10; }}  // GpType "Int" with "ephemeral generator".
                     },
                     {
                         {"Ant", "Int", {"Int", "Int"}},       // GpFunction "Ant", returns Int, takes two Int parameters.
                         {"Bat", "Int", {"Int", "Int"}},       // GpFunction "Bat", returns Int, takes two Int parameters.
                         {"Cat", "Int", {"Int"}}               // GpFunction "Cat", returns Int, takes one Int parameter.
                     }
                 };

Initially all random programs generated from this set consisted of exactly one Int constant. After making the fix to allow a type to be return by both functions and “ephemeral constants”, it produced trees of the given size (here 50):

Cat(Cat(Cat(Ant(Cat(Cat(Bat(Bat(Ant(4, Cat(7)), Ant(Cat(4), Cat(4))),
                            Cat(Cat(Bat(Bat(4, 8), Cat(Cat(Cat(8))))))))),
                Cat(Bat(Ant(Ant(1, Cat(7)), Ant(Cat(3), Cat(2))),
                        Ant(Bat(Cat(0), Cat(9)), Cat(Bat(7, Cat(4))))))))))

August 24, 2020

Component types GpType and GpFunction

I rewrote the prototype FunctionSet::makeRandomProgram() to be less ugly. Chiefly I made new abstractions, GpType and GpFunction, to represent types and functions of the GP FunctionSet. I added a new constructor for FunctionSet which allows the whole set of types and functions to be defined in a single expression. Before a lot of analysis of the function set (e.g. which functions return a value of this type?) was repeated each time it was needed. Now it all gets done once, in the new constructor, and cached. Similarly a lot of looking up character string names in maps has been replaced with direct pointers.

I also refactored the two pre-defined FunctionSets for testing: tiny_texsyn and full_texsyn.

August 17, 2020

Size control fixed for random programs

I tracked down the bug(s) that prevented exact control of the maximum size of GP programs constructed by FunctionSet::makeRandomProgram().  Now, generating a series of programs (here for the TexSyn FunctionSet) produces mostly programs of the given max_size (which is 50 in these examples), some slightly smaller, and occasionally much smaller. I have not decided if I care about the minimum size of these programs.

// size=50
Colorize(Vec2(3.337209, -0.111232), Vec2(-1.048723, 2.609511), SliceToRadial(Vec2(-0.735182, 2.328732), Vec2(2.607049, 4.752589), Blur(0.763175, Gamma(4.788119, EdgeDetect(0.303196, Blur(0.725915, Gamma(1.888874, Uniform(0.645293, 0.362680, 0.187303))))))), EdgeEnhance(0.566709, 0.395660, Min(BrightnessToHue(0.227292, EdgeDetect(0.088983, Uniform(0.432841, 0.452565, 0.759366))), Blur(0.878352, AdjustSaturation(0.648826, EdgeDetect(0.192719, Uniform(0.464628, 0.675937, 0.744247)))))))

// size=50
LotsOfSpots(0.012097, 0.135414, 0.751684, 0.965764, 0.281318, LotsOfSpots(0.147613, 0.588885, 0.570666, 0.800021, 0.687004, AdjustSaturation(0.277342, EdgeDetect(0.894000, Uniform(0.127598, 0.188189, 0.893133))), Blur(0.093948, Gamma(3.296728, Uniform(0.652457, 0.482005, 0.737463)))), LotsOfButtons(0.797039, 0.144344, 0.208901, 0.213856, 0.829122, Vec2(-1.575197, 1.251038), Uniform(0.904293, 0.052319, 0.090617), 0.854814, ColorNoise(Vec2(3.118072, 1.187010), Vec2(-0.589404, 2.754478), 0.299059)))

// size=49
Wrap(-3.596494, Vec2(0.694285, 0.919086), Vec2(0.989166, -4.823082), SliceShear(Vec2(-0.120761, -2.569393), Vec2(-0.134178, 1.804898), EdgeDetect(0.959444, Gamma(6.956436, Uniform(0.111692, 0.197541, 0.677295))), Vec2(2.580718, 0.258248), Vec2(3.048599, -3.998405), Min(BrightnessWrap(0.183154, 0.216393, EdgeEnhance(0.937688, 0.592261, Uniform(0.792651, 0.186018, 0.810909))), AbsDiff(Uniform(0.830450, 0.310026, 0.461115), Uniform(0.473002, 0.195799, 0.609615)))))

// size=8
ColorNoise(Vec2(4.320298, 0.666899), Vec2(2.787325, 4.352788), 0.550106)

// size=50
Multiply(Gamma(9.301153, EdgeDetect(0.117543, HueOnly(0.059045, 0.402121, Add(ColorNoise(Vec2(-0.885789, -2.376529), Vec2(4.686641, -0.853005), 0.158803), ColorNoise(Vec2(-0.682632, -3.960764), Vec2(0.204911, -0.370719), 0.662522))))), SliceGrating(Vec2(0.915037, 3.041960), Vec2(-3.293618, 4.275027), SoftMatte(Uniform(0.031453, 0.989732, 0.696574), Blur(0.835575, Uniform(0.979765, 0.764766, 0.473790)), BrightnessWrap(0.012443, 0.341328, Uniform(0.533497, 0.499851, 0.642036)))))

// size=20
AdjustSaturation(0.066990, Ring(4.104012, Vec2(-2.495622, 0.238659), Vec2(0.829247, -3.823189), AdjustBrightness(0.070340, ColorNoise(Vec2(-0.894583, 2.009082), Vec2(-4.681360, -2.824072), 0.809685))))

// size=4
Uniform(0.912225, 0.591371, 0.169519)

// size=49
LotsOfButtons(0.522967, 0.333162, 0.085013, 0.728105, 0.668366, Vec2(1.857913, -2.245440), ColorNoise(Vec2(-0.412046, -3.319272), Vec2(-4.977819, 2.511291), 0.610481), 0.917300, AdjustHue(0.857817, SoftMatte(Min(Uniform(0.211855, 0.353225, 0.061723), Uniform(0.792557, 0.015160, 0.339307)), Max(Uniform(0.163184, 0.786264, 0.147327), Uniform(0.351334, 0.191037, 0.729921)), AdjustSaturation(0.686154, ColorNoise(Vec2(0.018567, 4.154261), Vec2(3.782207, 4.571167), 0.044231)))))

// size=50
Ring(5.741549, Vec2(-0.906608, -4.878014), Vec2(2.884423, -3.600070), ColoredSpots(0.678892, 0.553492, 0.929361, 0.208069, 0.767077, CotsMap(Vec2(-3.395577, -0.600270), Vec2(2.026988, -3.274830), Vec2(0.036533, -4.649998), Vec2(2.966635, 1.534505), Uniform(0.527436, 0.518428, 0.101204)), Grating(Vec2(-1.834993, -0.729365), Uniform(0.231773, 0.243197, 0.261381), Vec2(2.077976, -3.491028), Uniform(0.279188, 0.504817, 0.897037), 0.532966, 0.978290)))

August 15, 2020

Prototype FunctionSet covering entire TexSyn API

Yesterday I plowed through the entire TexSyn API converting it into the prototype FunctionSet format. This includes 52 Texture operators, plus Vec2, plus several “ephemeral constants” for various random distributions of floating point values. This allowed procedural construction of random TexSyn programs. FunctionSet::makeRandomProgram() is still very much a prototype implementation, and still has a bug controlling program size. But I could at least print out the text of these random programs, then cut-and-paste that into TexSyn for rendering. Some samples of textures generated by these random programs are in today's entry in TexSyn's log.

August 13, 2020

Making random programs

I've been prototyping a FunctionSet class to represent the “domain specific language” manipulated by genetic programming. LazyPredator implements strongly typed genetic programming where the values of function and terminals, and the parameters to functions, all have associated types. I made a simple API for adding definitions of the types and the functions used in the “domain specific language”. These use prototype underpinnings, just enough scaffolding to begin developing additional functionality. After I “rough out” a working FunctionSet class, and so better understand the requirements, I will refactor the underlying FunctionSet structure to be more clean and efficient.

To initialize a GP population we need a utility—here called FunctionSet::makeRandomProgram()—to generate a “random program” in the “domain specific language” (aka a grammar) defined by a FunctionSet instance. By “random program” I mean a random expression, a composition of functions and terminals which, when evaluated, produce a value. makeRandomProgram() is further parameterized by a max_size for the generated programs. This size is measured as the count of function names and terminals such as numeric constants (and potentially input variables, but that is not currently supported).

This post is to mark that my prototype makeRandomProgram() is now generating random programs that are no longer obviously wrong. I made a toy FunctionSet corresponding to a tiny subset of TexSyn. The functions are drawn from: Vec2, Uniform, Affine, Multiply, and Scale. The terminals are float “ephemeral constants” whose values are randomly initialized. Here are a couple of “random programs” of size 20:

Scale(-1.89065,
      Affine(Vec2(2.71928, 1.51213),
             Vec2(-2.15447, 3.58087),
             Multiply(Scale(-0.46497,
                            Uniform(0.270371, 0.544808, 0.653164)),
                      Uniform(0.582032, 0.0811457, 0.593893))))

Affine(Vec2(1.62775, 0.925812),
       Vec2(0.892051, -2.5576),
       Scale(-3.9347,
             Affine(Vec2(1.14234, 0.321014),
                    Vec2(3.70146, 3.92498),
                    Uniform(0.842375, 0.46032, 0.180332))))

These are of course gibberish, not only because they are “random” but because this tiny function set is unable to express anything interesting. One important problem with the current code is that there is a bug in the control of program size. The max_size parameter is intended to be a strict upper bound. Instead FunctionSet::makeRandomProgram() generates programs whose sizes are distributed “in the vicinity of” max_size. That is at least better than a recent version that generated programs up to size 1000.

August 7, 2020

Monitor lifetime of Individual in Population

My vague plan is that the Population class will handle all aspects of Individuals. A Population instance will generate the initial collection of random programs. It will randomly select the individuals to participate in a tournament. It will form offspring from tournament winners, remove the losers, and replace them with the offspring.

One important bit of “owning” the individuals is that they must be properly allocated and de-allocated. I gave the Individual class a counter which gets incremented in the constructor and decremented in the destructor.

I made the first unit test which ensures that this count is initially zero, then constructing a Population with n Individuals causes it to be n, and that deleting the Population causes it to go back to zero. Right now it only tests the initial creation of (“mock”) Individuals, later the unit test should include running tournaments.

August 6, 2020

Getting started, stubs for Population, Individual, and UnitTests

Just starting to rough out the components of the system. Today it is a class for an evolutionary Population and the Individuals in it. Also a namespace for UnitTests with a goal of using “test driven development.”

This page, and the software it describes, by Craig Reynolds